MATEMATİĞİN aksiyomları denilen şeyler, matematiğin çıkış noktası için gerekli olan birkaç düşünce belirlemesidir. Matematik, büyüklüklerin bilimidir; onun hareket noktası, büyüklük kavramıdır. O, bunu, sakat bir biçimde tanımlar ve daha sonra tamımda mevcut olmayan aksiyomlar olarak dışardan alınan, büyüklüğün öteki ilkel belirlemelerini ekler, böylece tanıtlanmamış olarak görünürler ve doğaldır ki, matematiksel olarak da tanıtlanmamışlardır. Büyüklüğün tahlili, bütün bu aksiyom belirlemelerini, büyüklüğün gerekli belirlemeleri olarak verebilir. Spencer, bunların bize apaçık olarak göründükleri sürece, bu aksiyomların mirasla [sayfa 326] geçtiğini söylemekte haklıdır. Bunlar, diyalektik olarak, salt gereksiz yineleme olmadıkları ölçüde tanıtlanabilirler.
*
Matematik. Tüm matematik unsurlarından hiç biri, aritmetik işlemlerin dört türü arasmdaki farktan daha somut temellere dayanmış görünmemektedir. Ve çarpma daha başlangıçta, kısaltılmış bir toplama olarak, bölme aynı büyüklükteki sayılardan belirli bir eşit sayısal büyüklüklerin kısaltılmış çıkarması olarak kendini gösterir; bölme, bazan bölen bir kesir olduğu zaman tersine çevrilmiş kesirle çarparak, sağlanabilir. Cebir hesabında ise çok daha ileri gidilir. Her çıkarma (ab) toplama olarak (b+a), her bölme a/b, çarpma olarak a x 1/b gösterilebilir. Üslü büyüklüklerle hesap yapılırken, çok daha fazla ileri gidilir. Hesaplama çeşitleri arasındaki bütün katı farklılıklar ortadan kalkar, her şey karşıt biçimi içinde gösterilebilir. Bir üs kök olarak (x2 =
( . = +, : = + ,
Matematikte dönüm noktası, Descartes'ın değişken büyüklüğü olmuştu. Bununla birlikte, hareket ve bundan ötürü de diyalektik ve hemen ardından, Newton ve Leibniz tarafından bulunmamış olmakla birlikte, onlar tarafından tam olarak tamamlanan diferansiyel ve entegral hesapların zorunluluğu matematiğe girdi.
*
Nicelik ve nitelik. Sayı, bildiğimiz en saf nicel belirlemedir. Ama bu, nitel farklılıklarla doludur. 1. Hegel, sayı ve birim, çarpma, bölme, üssüne yükseltme, kök alma. Böylece, Hegel'de belirtilmeyen şey, nitel farklılıklar, asal sayılar ve katları, basit kökler ve üsler kendini gösterir. 16 yalnızca 16 tane birin toplamı değil, aynı zamanda 4'ün karesi, 2'nin dördüncü üssüdür. Daha fazlası. Asal sayılar, başka sayıların kendileriyle çarpımından meydana gelen sayılara yeni ve kesin nitelikler verirler: yalnız çift sayılar 2 ile bölünebilir ve aynı şey 4 ve 8 ile bölünme için de sözkonusudur. 3 için rakamların toplamı kuralı vardır ve çift sayılarla birleşme halinde, aynı şey, 9 ve 6 için de sözkonusudur. 7 için özel bir kural vardır. Bunlar, henüz bu işin başlangıcında olanlar için anlaşılmaz gibi görünen sayı oyunlarının temelini meydana getirir. O halde Hegel'in {Nicelik, s. 237) aritmetikte düşüncenin olmadığı konusundaki sözleri doğru değildir. Ama karşılaştırınız: "Ölçü".[213]
Matematik, sonsuz büyüklükten ve sonsuz küçüklükten sözettiği gibi, aşılması olanaksız nitel karşıtlık olarak ortaya çıkan bir nitelik farkını da kabul eder: [sayfa 328] nicelikler birbirleri arasında öylesine büyük farklılıklar gösterirler ki, aralarındaki her rasyonel bağıntı, her karşılaştırma nicel olarak kıyas kabul etmez bir halde son bulur. Sıradan oransızlığın, örneğin, çember ve düz çizgi oransızlığının buradaki durumu da diyalektik bir nitelik farkıdır; ama burada[1*] o, niteliğin farkını oransızlık noktasına kadar artıran benzer büyüklüklerin nicelik farkıdır.
*
Sayı. Tek başına sayı, sayı sistemi içinde bizzat bir nitelik alır ve nitelik kullanılan sisteme dayanır. 9, 1'in dokuz defa birbiriyle toplanmasından başka, 90, 99, 900.000 vb. sayılarının da temelidir. Bütün sayısal yasalar, seçilen sisteme dayanır ve onun tarafından belirlenir. İkili ve üçlü sistemde, 2x2 = 4 değildir, tersine, = 100, ya da, = 11'dir. Temel tek sayılarla ilgili bütün sistemlerde, tek ve çift sayılar arasındaki fark ortadan kalkar, örneğin 5 sistemine dayanınca 5 = 10, 10 = 20, 15 = 30. Bunun gibi aynı sistemde 3 ya da 9'un çarpımlarının 3n tam sayılarının toplamında da aynıdır (6 = 11,9 = 14). Demek ki temel sayı yalnız kendisinin niteliğini değil, bütün öteki sayıların niteliğini de belirliyor.
Sayıların üsleri bakımından sorun, daha da ileri gider: her sayı başka bir sayının üssü olarak kavranabilir tam ve kesirli sayılar kadar çok logaritma sistemleri vardır.
*
Bir. Birimi, ona tekabül eden çokluk ile bağıntı [sayfa 329] içersinde ve onun çokluktan gelen çeşitli köken biçimlerine uygun olarak incelediğimizde, nicel birimden daha basit ve ondan daha çok yanlı görünen bir şey yoktur. Her şeyden önce tüm pozitif sayı sisteminin taban sayısı birdir ve bu sayı sistemlerinin birbirlerine ardarda eklenmesiyle bütün öteki sayılar meydana gelir. Bir, bütün pozitif, negatif ve birin kesirli üslerinin ifadesidir: l2,
*
Sıfır, herhangi belirli niceliğin yadsıması olduğundan içerikten yoksun değildir. Tersine, sıfırın çok belirli bir içeriği vardır. Bütün pozitif ve negatif büyüklükler arasındaki sınır olarak, ne artı ve ne eksi olabilen biricik gerçek nötr sayı olarak, yalnızca çok belirli bir sayı olmakla kalmaz, aynı zamanda, kendisinin sınırlamış olduğu öteki bütün sayılardan kendi içinde daha önemlidir. Gerçekte sıfır, herhangi bir başka sayıdan, içerik yönünden daha zengindir. Başka herhangi bir sayının sağma konunca, sayı sistemimizde ona on katlı değeri verir. Sıfır yerine başka herhangi bir işaret de kullanılabilirdi, ama ancak bu işaretin, tek başına alındığı zaman sıfır anlamına gelmesi, = 0 olması koşuluyla. O halde sıfırın bu kullanılışı kendinde bulması ve tek başına onun böyle kullanılabilmesi, doğasında vardır. Sıfır, birlikte çarpıldığı başka her sayıyı yok eder. Bölen ya da bölünen olarak başka her sayı ile birleşince, onu birinci halde sonsuz büyüklükte, ikinci halde ise sonsuz küçüklükte bir duruma sokar; başka bir sayı ile sonsuz ilişkide bulunan tek sayıdır. 0/0, ∞ ile + ∞ arasındaki her sayıyı ifade edebilir ve her durumda [sayfa 331] gerçek bir büyüklüğü temsil eder.
Bir eşitliğin gerçek içeriği ancak, onun bütün öğeleri tek bir yana getirildiğinde açıkça ortaya çıkar. Böylece denklem, ikinci dereceden denklemlerde olduğu gibi sıfır değerine indirgenir ve bu, yüksek cebirde nerdeyse bir kuraldır. F (x, y) = 0 fonksiyonu bu durumda aynı z'ye eşit yapılabilir ve bu z = 0 olmasına karşın, normal bir bağımlı değişken gibi türevi alınır ve kısmî türevi belirlenir.
Her niceliğin hiçliği de nicelik olarak saptanabilir ve yalnız bu yüzden sıfırla hesap yapmak mümkündür. Yukardaki gibi sıfırla hiç çekinmeden hesap yapan, yani onunla belirli bir nicelik kavramı ile işlem yapan, onu başka nicel kavramlarla nicelik ilişkisine sokan matematikçiler, Hegel'de onu şöyle genelleştirilmiş bir halde okuyunca saçlarını yolarlar: hiç bir şeyin hiçliği belirli bir hiçliktir.
Gelelim (analitik) geometriye. Burada sıfır belirli bir noktadır; bu noktadan itibaren ölçüler bir çizgi boyunca, bir yönde pozitif, öteki yönde negatif olarak alınır. Demek ki burada sıfır, yalnız negatif ya da pozitif büyüklükle belirlenen her nokta gibi önemli değil, aynı zamanda, hepsinin bağımlı olduğu, hepsinin ilişkili bulunduğu, hepsinin belirlenmesini sağlayan nokta olarak çok daha büyük önem taşır. Hatta çoğu durumlarda tamamen isteğe bağlı olarak da alınabilir. Ama bir kez de alınırsa, bütün işlemin merkez noktası olarak kalır, öteki noktaların apsislerin bitim noktaları kaydedileceği çizginin yönünü bile belirler. Örneğin, dairenin denklemini elde etmek için, çevrenin Herhangi bir noktasını sıfır noktası olarak alırsak apsis doğrusu, dairenin merkezinden geçmek zorundadır. Bütün bunlar, hareketlerin hesaplanmasında da her kez alınan sıfır noktasının bütün işlemin baş ve kutup [sayfa 332] noktasını meydana getirdiği mekaniğe de aynı biçimde uygulanabilir. Termometrenin sıfır noktası, derecelerin istenilen sayısına bölünen ve böylece hem kendi kendisi içinde sıcaklık basamaklarının, hem de yüksek ya da düşük sıcaklığın ölçeği olarak hizmet gören sıcaklık bölümünün çok belirli alt sınırıdır. Demek ki, burada da, çok önemli bir noktadır. Termometrenin mutlak sıfırı bile, asla saf, soyut bir yadsımayı değil, maddenin çok belirli bir durumunu temsil eder: bu, moleküllerin kendi başına hareketinin son sınırının kaybolduğu ve maddenin yalnızca kütle olarak etki yaptığı sınırdır. Ne zaman sıfıra raslarsak, orada, sıfır, çok belirli bir şeyi temsil eder ve onun geometride, mekanikte vb. pratik olarak uygulanması, sınır olarak, kendisinin sınırladığı bütün gerçek büyüklüklerden daha önemli olduğunu tanıtlar.
*
Sıfır üsler. Logaritma dizilerindeki önemi:
başka bir özelliği yoktur. Bundan, birimin de, kendisiyle ne denli özdeş görünürse görünsün, herhangi bir başka sayının sıfır üssü olabildiğinden, içinde sonsuz çok yanlılık içerir ve bu çeşitlilik, birimin belirlenmiş bir birim olarak, bu süreçle bağlantı içinde (anlık [sayfa 333] büyüklük ya da bir değişkenin biçimi olarak) sürecin değişken sonuçlarından biri olarak bulunduğu her fırsatta tanıtlanan sanal bir şey değildir.
*
*
Matematik. Belirli bir büyüklüğü, örneğin bir iki terimliyi, sonsuz bir dizi, yani belirli olmayan bir şey içersinde çözmek sağduyuya saçma gözükür. Ama sonsuz diziler ve iki terimli (binome) teorem olmasaydı şimdi nerede bulunurduk? [sayfa 334]
*
Asimtotlar. Geometri, doğru ve eğrinin mutlak karşıtlıklar olduğunun, doğrunun eğri içinde ve eğrinin doğru içinde kesenkes ifade edilemezliğinin, ikisinin kıyaslanamazhğınm keşfedilmesiyle başlar. Ve hatta dairenin hesaplanması da, ancak çemberinin doğru çizgiler halinde ifadesiyle mümkündür. Asimtotlu eğrilerde ise doğru eğrinin içinde ve eğri doğrunun içinde kaynaşır; paralellik kavramı da tıpkı böyledir: çizgiler paralel değildir, birbirlerine sürekli olarak yaklaşırlar ve hiç bir zaman kesişmezler; eğrinin kolu gittikçe daha çok doğrulaşır ama hiç bir zaman tamamen doğru hale gelmez, tıpkı analitik geometride olduğu gibi, doğru çizgi sonsuz küçüklükte bir eğri olarak birinci derecede bir eğri gibi kabul edilir. Logaritmik eğrinin -x'i, ne kadar büyük olursa olsun, y asla = 0 olamaz.
*
Diferansiyel hesaplarda doğru ile eğri, son aşamada eşit olur: diferansiyel üçgende hipotenüs, yayın diferansiyelini meydana getirir (tanjant yönteminde), bu hipotenüs "aynı zamanda hem yayın unsuru ve hem de tanjantın unsuru olan küçük oldukça doğru çizgi olarak" kabul edilebilir eğri, ister doğru çizgilerin sonsuz sayıdaki toplamı olarak görülsün, ister "tam bir eğri olarak kabul edilsin", "eğri M'nin her noktasında sonsuz küçüklükte olduğundan, eğrinin unsurunun tanjant unsuruna olan son oranının, eşitliğin bir oranı olduğu açıktır".[2*] Böylece oran, sürekli olarak eşitliğe yaklaşmasına, ama eğrinin mahiyetine uygun olarak [sayfa 335] asimtot biçiminde yaklaşmasına karşın, dokunma, gene de uzunluğu olmayan tek bir nokta ile sınırlandığı için, doğrunun ve eğrinin sonunda eşitliğe ulaştığı varsayılır. (Bossut, Calcul diff. et integr., Paris, An VI, I, s. 149.)[215] Kutupsal eğrilerde,[216] sanal diferansiyel apsisler, her ikisi kutupta kesişmelerine karşın, gerçek apsislere paralel kabul edilir ve işlemler buna dayandırılır; gerçekten de, bundan, iki çizginin kesişme noktasında belirgin bir açı yapan iki üçgenin benzerliği, benzerliğin bütün temelini meydana getiren paralellik çıkartılır. (Şekil 17.)[217]
Doğru ve eğri çizgilerin matematiği, böylece oldukça sona yaklaşınca, eğriyi doğru olarak alan (diferansiyel üçgen) ve doğruyu eğri olarak gören (sonsuz küçüklükte eğri olan birinci dereceden eğri çizgi) matematik sayesinde, yeni ve hemen hemen sonsuz bir alan açılıyor. Vah metafizik!
*
Trigonometri. Sentetik geometri, bir üçgenin özelliklerini ele alıp bitirdikten ve artık söyleyecek yeni bir şeyi kalmadıktan sonra, çok basit ve tamamen diyalektik işlem yoluyla çok daha geniş bir ufuk açılıyor. Artık üçgen, kendisinde ve kendisi için değil, başka bir şekille, daire ile ele alınıyor. Her dik açılı üçgen, bir dairenin parçası olarak alınabilir: eğer hipotenüs = r ise, dik açıya bitişik kenarlar sinüs ve kosinüstür, kenarlardan biri 5 = r ise, öteki kenar = tanjant, hipotenüs = sekanttır. Bu yolla, kenarlar ve açılar, oldukça farklı verilince, üçgenin daire ile bu bağıntısı olmaksızın keşfi ve kullanılması olanaksız olan belirli ilişkiler, ve oldukça yeni bir üçgen teorisi ortaya çıkmaktadır; ki bu teori, eskisini aşmakta ve evrensel olarak uygulanabilir [sayfa 336] olmaktadır, çünkü her üçgen iki dik açılı üçgenlere dönüştürülebilmektedir. Trigonometrinin sentetik geometriden bu' gelişimi, diyalektiğin güzel bir örneği, şeyleri kendi içlerinde yalıtlamaları yerine onların iç bağıntılarında kavranılması yoludur.
*
Özdeşlik ve fark. dx'in sonsuz küçük, ama gerçekten etkili ve her şeyi yapacak nitelikte olduğu diferansiyel hesapta diyalektik ilişki, halen görülmektedir.
*
Molekül ve diferansiyel. Wiedemann (III, s. 636),[218] sonlu ve molekülsel uzaklıkları birbirine doğrudan karşıt olarak koyuyor.
*
GERÇEK DÜNYADA MATEMATİK SONSUZLUĞUN
İLKÖRNEKLERİ ÜZERİNE[219]
S. 1718[3*] İÇİN: DÜŞÜNCE VE VARLIĞIN UYUMU.
MATEMATİĞİN SONSUZLUĞU
Öznel düşüncemizin ve nesnel dünyanın aynı yasalara bağlı bulunduğu ve bundan dolayı da her ikisinin de son tahlilde, sonuçlarında birbirleriyle çelişemeyecekleri, tersine birbirinin içine girmek zorunda oldukları olgusu, tüm teorik düşüncemizi mutlak biçimde egemenliği altında tutar. Bu, teorik düşünce yolunda, bilinçsiz ve koşulsuz bir öncüldür. 18. yüzyıl materyalizmi, [sayfa 337] genellikle metafizik bir nitelik taşıması dolayısıyla, bu öncülü yalnızca içeriği bakımından incelemiştir. Bu materyalizm, her düşüncenin ve bilginin içeriğinin duyusal deneyden çıkması gerektiği kanıtında sınırlı kalıyor ve şu ilkeyi yeniden koyuyordu: Nihil est in intellectu, quod non fuerit in sensu.[220] Önce modern idealist, ama aynı zamanda diyalektik olan felsefe ve özellikle, onu biçim yönünden de ilk kez inceleyen Hegel. Burada karşımıza çıkan sayısız keyfî yapılara ve kurgulara karşın, sonucunun biçiminin idealist şekilde başaşağı edilmesine, düşünce ile varlığın birliğine karşın, bu felsefenin, düşünce süreçlerinin doğanın ve tarihin süreçlerine ve doğanın ve tarihin süreçlerinin düşünce süreçlerine benzer olduğunun birçok durumlarda ve en farklı alanlarda bu süreçlerin tümünde benzer yasaların geçerli olduğunun tanıtlanması yadsınamaz. Öte yandan modern doğabilim, içeriğini, eski metafizik sınırlama ve formülasyonu darmadağın edecek bir yolda deneyden hareketle bütün düşünce içeriğinin kökeninin ilkesini genişletmiştir. Kazanılmış özelliklerin kalıtımla geçmesini kabul ederek deneme konusunu bireyden türe kadar yaygınlaştırıyor; tek bir bireyin deneyinin yerini, belirli bir ölçüde, bir dizi atalarının deneylerinin sonuçlan ile değiştirerek tek bireyin deneyinin artık gereksiz olduğunu ortaya koyuyor. Örneğin, bizim aramızda matematiksel aksiyomlar sekiz yaşındaki her çocuk için kendiliğinden açık göründüğünden, bunların deneyle tanıtlanmasının gereği yoktur; bu, salt "birikmiş kalıtımın" sonucudur. Bir vahşiye ya da Avustralyalı zenciye bunları tek bir kanıtla öğretmek ise çok zordur.
Elimizdeki yapıtta[4*] diyalektik bütün hareketin en [sayfa 338] genel yasalarının bilimi olarak alınmıştır. Aynı zamanda bu demektir ki, onun yasaları, düşüncenin hareketi için olduğu kadar, doğada ve insan tarihindeki hareket için de geçerli olmalıdır. Böyle bir yasa, bu üç alanın ikisinde, hatta her üçünde, metafizik darkafalılığın tanıdığı şeyin bir ve aynı yasa olduğu konusunda bir açıklığa varmasına gereklilik kalmadan kabul edilebilir.
Bir örnek alalım. Kuşkusuz bütün teorik ilerlemeler arasında insan aklının en büyük zaferi, 17. yüzyılın ikinci yarısında, sonsuz küçüklük hesabının keşfedilmesidir. İnsan aklının saf ve müstesna bir ustalığı söz-konusuysa, bu, işte buradadır. Sonsuz küçüklük hesaplarında kullanılan büyüklüklerin çeşitli derecelerdeki diferansiyellerin ve sonsuzların çevresini bugün de saran sır, burada üzerinde durduğumuz şeylerin insan zekâsının saf "özgür yaratmaları ve tasarlamaları" olduğunu, nesnel dünyada buna uyan bir şeyin bulunmadığının hâlâ daha hayal edildiği konusunda en iyi kanıttır. Oysa durum bunun tersidir. Bütün bu sanal büyüklüklerin örneklerini doğa verir.
Geometrimiz uzay bağıntılarını, aritmetik ve cebirimiz de sayısal büyüklükleri hareket noktası alır, bunlar yersel koşullarımıza, ve bu nedenle de mekaniğin kütleler dünyada görülen ve insanlar tarafından hareket ettirilen kütleler olarak deyimlendirdiği cisimlerin büyüklüklerine tekabül ederler. Bu kütleler karşısında dünya kütlesi sonsuz büyüklükte görünür ve yersel mekanik tarafından da sonsuz büyüklük olarak ele alınır. Dünyanın yarıçapı = ∞, düşme yasasında, bu, bütün mekaniğin temel ilkesidir. Ama yalnız dünya değil, bütün güneş sistemi ve onunla ilgili uzaklıklar, bize ancak teleskopla görünebilen yıldızlar sisteminde ışık yılları diye bilinen uzaklıklarla uğraşmaya [sayfa 339] başladığımızda, sonsuz denecek kadar küçük görünürler. O halde burada yalnızca birinci dereceden değil, ikinci dereceden bir sonsuzluk söz konusudur, sonsuz uzayda daha yüksek derecelerde daha başka sonsuzlukların kurulmasını, eğer istekleri varsa, okurlarımızın hayal gücüne bırakabiliriz.
Bugün fizikte ve kimyada egemen olan görüş gereğince, yersel kütleler, mekaniğin ele aldığı cisimler, moleküllerden bu cismin fiziksel ve kimyasal özdeşliğini ortadan kaldırmaksızın daha fazla parçalanamayacak olan en küçük parçacıklardan meydana gelmiştir. W. Thomson'un hesaplarına göre, bu moleküllerden en küçüğünün çapı milimetrenin elli milyonda-birinden daha küçük olamaz.[221] Ama en büyük molekülün bir milimetrenin yirmi beş milyonda-biri kadar bir çapa eriştiğini kabul etsek bile, mekanik, fizik ve hatta kimyanın ele aldığı en küçük kütle ile karşılaştırıldığında sonsuz denilecek kadar küçük bir büyüklük gene de vardır. Bununla birlikte, sözü edilen kütleye özgü bütün özellikler bu molekülde vardır, bu molekül, fiziksel ve kimyasal olarak kütleyi temsil edebilir ve bütün kimyasal denklemlerde kütleyi gerçek bir temsil yeteneğine sahiptir. Kısacası, matematiksel diferansiyelin kendi değişkenliklerine olan bağıntısı gibi, molekülün de ona tekabül eden kütleyle bağıntısında aynı özellikler vardır. Tek fark, diferansiyelde, matematiksel soyutlamada gizemli ve anlaşılmaz görünen şeyin burada olağan ve apaçık olmasıdır.
Doğa, bu diferansiyellerle, moleküllerle, matematiğin soyut diferansiyellerle uğraşırken uyguladığı biçimde ve tamamen aynı yasalar çerçevesinde uğraşır. Böylece, örneğin, x3 = 3x2dx diferansiyelinde, 3xdx2 ve dx3 hesaba katılmaz. Bunu geometrik olarak kurarsak, kenar uzunluğu sonsuz küçüklükteki dx büyüklüğü kadar [sayfa 340] büyütülen" x uzunluğunda kenarları olan bir küp ortaya çıkar. Bu küpün süblime olmuş bir elementten, diyelim ki kükürtten meydana geldiğini varsayalım; aynı köşede birleşen üç yüzeyin korunduğunu, öteki üçünün serbest olduğunu düşünelim. Şimdi bu kükürt küpü, sülfür gazı atmosferi içine koyar ve sıcaklığı gerektiği kadar düşürürsek, kükürt küpün üç serbest yüzeyi üzerinde yığılır. Süreci en saf durumda belirlemek için, bu üç yüzün herbirinde önce bir molekül kalınlığında bir tabaka toplandığını varsayarsak, fizik ve kimyada tamamen geçerli bir işlem biçimi içinde kalırız. Küpün x kenar uzunluğu, bir dx molekülünün çapı kadar büyümüştür. Küpün hacmi x3 ile x3 + 3x2dx + 3xdx2 + dx3 arasındaki fark kadar büyümüştür; burada biz dx3 tek bir molekülü, ve 3xdx2 düz sırada yanyana gelmiş moleküllerden meydana gelen x + dx uzunluğunun üç sırasını, matematiksel aynı gerekçe ile ihmal edebiliriz. Sonuç aynıdır: küpün kütlesindeki artış 3x2dx'tir.
Daha kesin bir ifadeyle, iki ya da üç molekül aynı sahada bulunamayacaklarından, kükürt küpünde dx3 ve 3xdx2 meydana gelmez ve küpün kütlesindeki artış da bu yüzden tam 3x2dx + 3xdx'tir. O halde bunun açıklaması, matematikte dx'in çizgisel bir büyüklüğü olduğu, kalınlığı ve genişliği bulunmayan aynı çizgilerin ise bilindiği gibi doğada kendi başına ortaya çıkmadığı, bunun için matematiksel soyutlamaların da yalnız saf matematikte kayıtsız şartsız geçerli oldukları biçimindedir. Bu sonuncu da 3xdx2 + dx3ü ihmal ettiğinden ortada bir fark yoktur.
Buharlaşmada da böyledir. Bir bardak suda en üst molekül tabakası buharlaşınca, su tabakasının yüksekliği olan x, dx kadar azalır ve bir molekül tabakasının birbiri ardından sürekli buharlaşması gerçekten [sayfa 341] sürekli bir farklılaşmadır. Kızgın buhar, basınç ve soğutma yoluyla bir kapta tekrar su halinde yoğunlaşırsa, bir molekül tabakası kap doluncaya kadar başka bir tabakanın üstüne gelirse (bu arada sürecin saflığını yokeden yan koşullan gözden uzak tutabiliriz), burada ancak bir tanesi insan kafası ile bilinçli olarak meydana getirilerek ve öteki de bilinçsiz olarak doğa tarafından gerçekleştirilerek farklı hale gelen kesin bir entegrasyon meydana gelmiş demektir.
Ama sonsuz küçüklük hesaplarına tam olarak benzeşen süreçler, yalnızca sıvı halden gaz haline ve gaz halinden sıvı hale geçişte görülmekle kalmaz. Kütle hareketi çarpma yoluyla durumunu yitirir ve ısı, molekül hareketi biçimine dönüşürse, kütle hareketinin farklılaşmasından başka bir şey mi olur? Buhar makinesinin silindirinde buharın molekül hareketleri, pistonları belli ölçüde kaldıracak, kitle hareketine dönüşecek gibi birbirine eklenirse, entegre edilmiş değil midir? Kimya, molekülleri atomlara, daha küçük kütlelere ve aralarındaki boşlukları daha çok bırakacak şekilde ama aynı derecede büyüklüklere, öyle ki ikisi de belirli, birbirlerine karşı sonlu bağıntılar olacak şekilde parçalar. Bundan dolayı, cisimlerin molekül yapısını ifade eden bütün kimyasal denklemler, biçim bakımından diferansiyel denklemlerdir. Ancak gerçekte bunlar, onlarda temsil edilen atom ağırlıkları dolayısıyla zaten entegrasyona tâbi olmuşlardır. Çünkü kimya, bilinen karşılıklı bağıntıların büyüklüklerini diferansiyelle (türevle) hesaplar.
Bununla birlikte, atomları, hiç bir zaman basit ya da genellikle bilinen en küçük madde parçacıkları olarak kabul etmek doğru değildir. Atomların bileşik olduğu görüşüne giderek daha çok eğilim gösteren kimya bir yana, fizikçilerin çoğu, ışığı ileten ve ısıyı yayan [sayfa 342] evrensel esirin de kimyasal atomların ve fiziksel moleküllerin mekanik kütlelere olan bağıntısı gibi, yani d2x'in dx'e olan bağıntısı gibi bağıntısı olan çok küçük ayrı parçacıklardan oluştuğunu ileri sürmektedirler. Demek ki, burada, maddenin yapısı konusundaki yaygın görüşte de, ikinci dereceden bir diferansiyel vardır ve bundan hoşlanan herhangi bir kimsenin d3x, d4x vb. gibi benzeşimlerin doğada da bulunması gerektiğini düşünmemesi için hemen hiç bir neden yoktur.
O halde maddenin yapısı konusunda nasıl bir görüşe sahip olunursa olunsun, madde, kesindir ki, göreli olarak farklı kütle niteliğindeki iyi belirlenmiş bir dizi gruplara ayrılmıştır; öyle ki bu her farklı grubun öğeleri, birbirleri karşısında belirli, sonlu bir kütle orantısındadır; bu gruplar, matematiksel anlamda bir sonraki grubun, sonsuz büyüklükte ya da sonsuz küçüklükteki oran halinde bulunmasının tersinedir. Görünebilen yıldızlar sistemi, güneş sistemi, yersel kütleler, moleküller ve atomlar, son olarak esir parçacıkları, hep böyle birer grup meydana getirirler. Bu, ayrı gruplar arasında ara halkalar bulunması durumunu değiştirmez. Böylece güneş sisteminin kütleleri ile yersel kütleler arasında yıldızsılar (ki bunlardan bazılarının çapı, örneğin Reuss prensliğinin yeni kolundan daha büyük değildir[222], göktaşları vb. bulunur. Böylece organik âlemde yersel kütlelerle moleküller arasında hücre bulunur. Bu ara halkalar, ancak, doğada sıçrama olmadığını tanıtlar, çünkü doğa tümüyle sıçramalardan meydana gelmiştir.
Matematik, gerçek büyüklüklerle hesap yaptığı ölçüde, aynı zamanda bu görüş tarzını da çekinmeden kullanır. Yersel mekanik için dünya kütlesi sonsuz büyüklük olarak kabul edilir, bunun gibi gökbilim için de yersel kütleler ve onlara tekabül eden göktaşları [sayfa 343] sonsuz küçük olarak kabul edilir ve aynı şekilde güneş sisteminin gezegenlerinin uzaklıkları ve kütleleri, gökbilim için, en yakın sabit yıldızların ötesine uzanan yıldızlar sistemimizin yapısını incelemeye başlar başlamaz, hiç bir anlam taşımaz. Ama matematikçiler soyutlamanın fethedilmez kalesine, saf denilen matematiğe çekilince, bütün bu benzeşimler unutulur, sonsuz, tümüyle gizemli bir şey haline gelir, onunla ilgili işlemlerin yapılışı salt kavranmaz bir şey, her türlü deney ve tüm mantığa aykırı bir şey olarak görünür. Matematikçilerin kendi işlem tarzlarını açıklamaktan çok, bunları mazur gösteren, her zaman dikkat çekici bir yeterlikte doğru sonuçlar sağlayan ahmaklık ve saçmalıklar, örneğin Hegel'in doğa felsefesi konusunda, matematikçilerin ve doğabilimcilerin onların dehşetini hiç bir zaman yeterince ifade edemedikleri en kötü görüntüleri ve gerçek fantezileri aşar. Soyutlamaları en aşırı noktaya götürdüğü için Hegel'i suçladıkları halde, aynı şeyi daha geniş ölçüde kendileri yapıyorlar. Saf denilen tüm matematiğin soyutlamalarla uğraştığını, onun bütün büyüklüklerinin, kesin bir deyişle, sanal büyüklükler olduğunu, aşın noktaya kadar götürülen bütün soyutlamaların saçmalığa ya da karşıtlığa dönüştüğünü unuturlar. Matematiksel sonsuzluk, bilinçsiz bile olsa, gerçeklikten alınmıştır ve bundan dolayı da kendi kendisiyle değil, yalnız gerçekle, matematiksel soyutlama ile açıklanablir. Gördüğümüz gibi, gerçeği bu bakımdan incelersek, gerçek ilişkilere varırız; matematiksel sonsuzluk ilişkisi, hatta bu ilişkinin etkilediği matematiksel yolun doğal benzeşimleri bu ilişkilerden çıkar. Böylece konu açıklanmış olur.
(Haeckelin düşünce ve oluş özdeşliğinin kötü bir yinelenmesi. Ama aynı zamanda sürekli ve kesikli madde arasındaki çelişki; bkz: Hegel.)[223] [sayfa 344]
Diferansiyel hesap, ilk kez olarak, yalnızca durumları değil süreçleri de matematiksel olarak temsil etmeyi, doğabilim için olanaklı kılmıştır: hareket.
*
Matematiğin uygulanması: katı cisimlerin mekaniğinde mutlaktır, gazların mekaniğinde yaklaşıktır, akışkanların mekaniğinde şimdiki durumda daha zordur fizikte daha çok deneme ve bağıntı aşamasındadır kimyada, birinci dereceden ve en basit yapıda basit denklemlerdir, biyolojide = 0. [sayfa 345]
[1*] Yani sonsuzluğun matematiğinde. -Ed.

[2*] İtalikler Engels'indir. -Ed.

[3*] Bkz: Anti-Dühring, Sol Yayınları, Ankara 1977, s. 53-54. -Ed.

[4*] Yani Anti-Dühring'de, s. 240-141. -Ed.

[213] Birinci nokta için Engels, Hegel'in, aritmetikte düşüncenin "düşüncesizlik" içinde hareket ettiği (Mantık Bilimi, kitap I, bölüm II, kısım 2, felsefî kavramların anlatılması için sayısal belirlenimlerin üzerine gözlem) sözlerini kastediyor; ikinci nokta için ise, Hegel'in, "doğal sayı sistemi, şimdiden, salt dışsal ilerleme içinde kendini gösteren nitel unsurlarla ilgili böyle bir düğüm çizgisi gösterir" vb. (aynı yapıt, bölüm III, kısım 2, ölçü ilişkilerinin düğüm çizgilerinin örnekleri üzerine gözlem; natura non facit saltum) deyişini kastediyor. -328.

[214] Bu deyim, Engels'in "Doğru ve Eğri" parçasında belirttiği, Bossut'un kitabında vardır. Bossut, "Bitimli Farklarla' Entegral Hesap" bölümünde, özellikle şu problemi inceler: "x değişken büyüklüğün tüm sayılı basamaklarını entegre etmek ya da toplamak." Bossut Dx farkının değişmez olduğunu kabul ediyor ve onu w Yunan harfi ile gösteriyor, w'nin ya da w toplamı x'e eşit olduğundan, w x 1 ya da x°'ın toplamı da x'e eşittir. Bossut bu denklemi Swx° = x biçiminde yazar, w değişmesini dışarda bırakır ve toplama işaretinin önüne koyar, wSx° = x formülünü elde eder ve bundan da Sx° = x/w denklemi çıkar. Bossut bu son denklemi daha sonra Sx, Sx2, Sx3 vb. büyüklüklerini bulmak ve başka ödevleri çözmek için kullanılır. Bkz: Bossut, Traités de Calcul différentiel et de Calcul intégral, t. I, Paris 1798, s. 38. - 333.

[215] Ch. Bossut, Traités de Calcul différentiel et de Calcul intégral, 1.1, Paris, an VI (1798), s. 149. -336.

[216] Karşılıklı koordinatlar sisteminde düşünülen eğrileri Bossut'un nasıl adlandırdığım gösteriyor. -336.

[217] Engels, Bossut'un Troites'sinin 148-51. sayfalarındaki 17. şekli ve bunun açıklamasını kastediyor. Bu şeklin biçimi şöyledir:
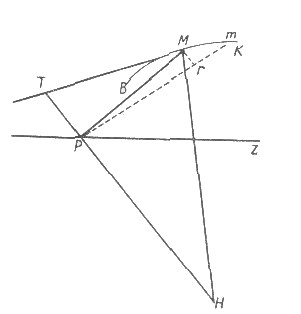
BMK eğridir. MT onun tanjantıdır. P, koordinatların kutbu ya da orijinidir. PZ kutupsal eksendir. PM, M noktasının ordinatıdır (Engels buna "gerçek apsis" diyor; günümüzde ise yarıçap vektörü diye adlandırılıyor). Pm, M'ye son derece yakın olan m noktasının ordinatıdır (Engels bu yarıçap vektörü için "diferansiyel sanal apsis" diyor). MH, MT tanjantına diktir. TPH, MP ordinatına diktir. Mr, PM yarıçapı ile gösterilen eğridir MPm son derece küçük bir açı olduğundan, PM ile Pm paralel kabul edilir. Mrm ve TPM üçgenleri de Mrm ve MPH üçgenleri benzer üçgenler olarak kabul edilir. -336.

[218] Bkz: 95 numaralı not. -337. 
[219] Bu not, Engels'in Doğanın Diyalektiği malzemesinin ikinci dosyasına koyduğu üç büyük nottan (Noten) biridir (Bkz: 204 sayılı not). Önce [Anti]-Dühring'in ilk baskısının 17-18. sayfalarına bir açıklama notunun ilk taslağı olarak yazılmıştır. "Gerçek Dünyada Matematiksel Sonsuzluğun İlk örnekleri Üzerine" başlığı, Doğanın Diyalektiği''nin ikinci dosyasının içindekiler listesine Engels tarafından konmuştur, "s. 17-18 için; Düşünce ve Oluşun Uyumluluğu. Matematiğin Sonsuzluğu" altbaşlığı, notun başlangıcında vardır. -337. 
[220] Nihil est in intellectu, quod non fuerit in sensu (duyularda olmayan bir şey zihinde de yoktur), duyumculuğun temel ilkesidir. Bu ilkenin içeriği Aristoteles'e kadar gider (bkz: Aristoteles'in Posterior Analytics'i). -338. 
[221] Bu rakam, önce 31 Mart 1870 tarih ve 22 sayılı Nature'da, daha sonra da Thomson ve Tait'ın Treaüse on Natura! Philosophy adlı yapıtının ikinci baskısında (Vol. I, Part II, New ed., Cambridge 1883, s. 501-52) ek olarak yayınlanan "The Size of Atoms" (Atomların Büyüklüğü) başlıklı bir makalede William Thomson tarafından verilir. - 340. 
[222] 1871'den sonra Alman İmparatorluğunu meydana getiren cüce devletlerden biri. -343. 
[223] Engels, olası ki, burada Haeckel'in psikofiziksel monizmine ve onun maddenin yapısı ile ilgili görüşlerine değiniyor. Engels'in [Anti]-Dühring'e ikinci notunda belirttiği Die Perigenesis der Plastidule'de Haeckel, örneğin, temel "ruh"un yalnız "plastidüler"de, ya da protoplazma moleküllerinde değil, aynı zamanda atomlarda var olduğunu ve bütün atomların "canlı" olduğunu, "duyum" ve "iradeye" sahip bulunduklarını kabul eder. Aynı kitapta Haeckel, atomları mutlak ayrı, mutlak bölünmez ve mutlak değişmez bir şey olarak tanımlar, bunun yanında da ayrı atomlarla esirin varlığını mutlak sürekli bir şey olarak tanır (aynı yapıt, Berlin 1876, s. 38-40).
Engels, "Maddenin Bölünebilirliği" notunda, HegeFin maddenin sürekliliği ve kesikliği çelişkisini nasıl işlediğini belirtir. -344. 
